# 机器学习-常见算法

作者：华王
星球：https://t.zsxq.com/0dgMjetVg (opens new window)

学习、分享、成功；提高效率，有所收获！😄

# 一 K-近邻算法(KNN)

1.1简介

K Nearest Neighbor算法又叫KNN算法，这个算法是机器学习里面一个比较经典的算法

根据你的“邻居”来推断出你的类别

定义：

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

两个样本的距离可以通过如下公式计算，又叫欧式距离

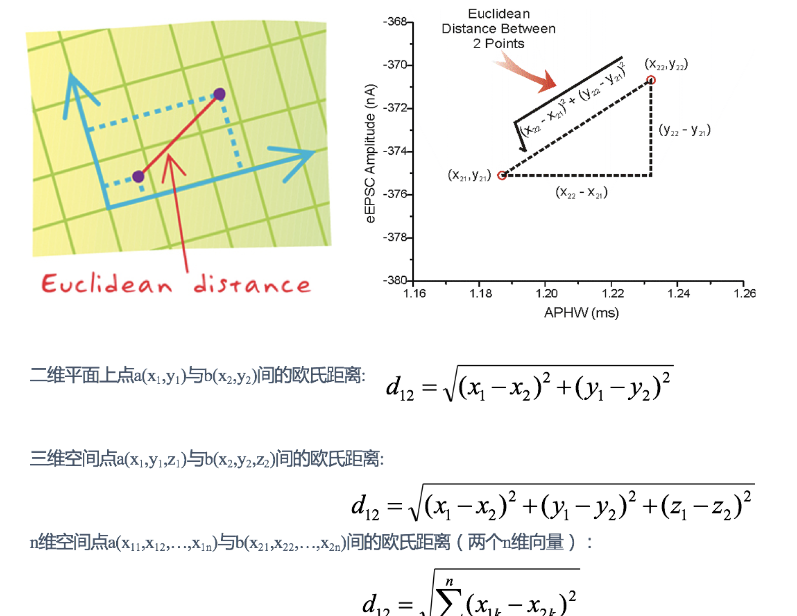
1.2 代码示例

def knncls():
    """
    K近邻算法预测入住位置类别
    :return:
    """
    # 一、处理数据以及特征工程
    # 1、读取收，缩小数据的范围
    data = pd.read_csv("./data/FBlocation/train.csv")

    # 数据逻辑筛选操作 df.query()
    data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")

    # 删除time这一列特征
    data = data.drop(['time'], axis=1)

    print(data)

    # 删除入住次数少于三次位置
    place_count = data.groupby('place_id').count()

    tf = place_count[place_count.row_id > 3].reset_index()

    data = data[data['place_id'].isin(tf.place_id)]

    # 3、取出特征值和目标值
    y = data['place_id']
    # y = data[['place_id']]

    x = data.drop(['place_id', 'row_id'], axis=1)

    # 4、数据分割与特征工程?

    # （1）、数据分割
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

    # (2)、标准化
    std = StandardScaler()

    # 队训练集进行标准化操作
    x_train = std.fit_transform(x_train)
    print(x_train)

    # 进行测试集的标准化操作
    x_test = std.fit_transform(x_test)

    # 二、算法的输入训练预测
    # K值：算法传入参数不定的值    理论上：k = 根号(样本数)
    # K值：后面会使用参数调优方法，去轮流试出最好的参数[1,3,5,10,20,100,200]
    knn = KNeighborsClassifier(n_neighbors=1)

    # 调用fit()
    knn.fit(x_train, y_train)

    # 预测测试数据集，得出准确率
    y_predict = knn.predict(x_test)

    print("预测测试集类别：", y_predict)
    print("准确率为：", knn.score(x_test, y_test))
    return None

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

1.3 优缺点

优点：简单，易于理解，易于实现，无需训练

缺点：懒惰算法，对测试样本分类时的计算量大，内存开销大，必须指定K值，K值选择不当则分类精度不能保证

使用场景：小数据场景，几千～几万样本，具体场景具体业务去测试

1.4 补充：

交叉验证(cross validation)

将拿到的训练数据，分为训练和验证集。以下图为例：将数据分成5份，其中一份作为验证集。然后经过5次(组)的测试，每次都更换不同的验证集。即得到5组模型的结果，取平均值作为最终结果。又称5折交叉验证。

超参数搜索-网格搜索(Grid Search)

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

# 二朴素贝叶斯算法

例如：垃圾邮件分类就是使用这种算法

概率：定义为一件事情发生的可能性

贝叶斯公式

代码示例：20类新闻分类

def nbcls():
    """
    朴素贝叶斯对新闻数据集进行预测
    :return:
    """
    # 获取新闻的数据，20个类别
    news = fetch_20newsgroups(subset='all')

    # 进行数据集分割
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.3)

    # 对于文本数据，进行特征抽取
    tf = TfidfVectorizer()

    x_train = tf.fit_transform(x_train)
    # 这里打印出来的列表是：训练集当中的所有不同词的组成的一个列表
    print(tf.get_feature_names())
    # print(x_train.toarray())

    # 不能调用fit_transform
    x_test = tf.transform(x_test)

    # estimator估计器流程
    mlb = MultinomialNB(alpha=1.0)

    mlb.fit(x_train, y_train)

    # 进行预测
    y_predict = mlb.predict(x_test)

    print("预测每篇文章的类别：", y_predict[:100])
    print("真实类别为：", y_test[:100])
    print("预测准确率为：", mlb.score(x_test, y_test))
    return None

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 三逻辑回归

逻辑回归（Logistic Regression）是机器学习中的一种分类模型，逻辑回归是一种分类算法，虽然名字中带有回归。由于算法的简单和高效，在实际中应用非常广泛。

使用场景：广告点击率；是否为垃圾邮件；是否患病；金融诈骗；虚假账号

逻辑回归原理

1 输入

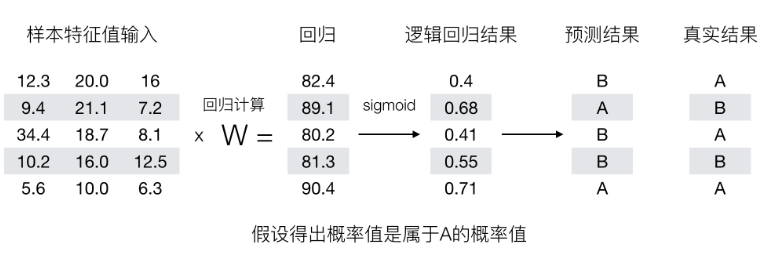
逻辑回归的输入就是一个线性回归的结果

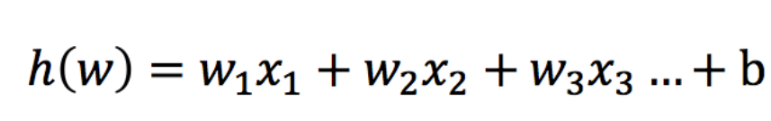
2 激活函数

sigmoid函数

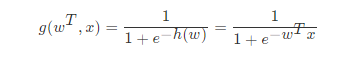
回归的结果输入到sigmoid函数当中；输出结果：[0, 1]区间中的一个概率值，默认为0.5为阈值

结果解释(重要)：假设有两个类别A，B，并且假设我们的概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果0.55，那么这个概率值超过0.5，意味着我们训练或者预测的结果就是A(1)类别。那么反之，如果得出结果为0.3那么，训练或者预测结果就为B(0)类别

3 损失与优化

使用梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数，提升原本属于1类别的概率，降低原本是0类别的概率

4 肿瘤预测案例

# 1.获取数据
names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
                   'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']

data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
                  names=names)
data.head()
# 2.基本数据处理
# 2.1 缺失值处理
data = data.replace(to_replace="?", value=np.NaN)
data = data.dropna()
# 2.2 确定特征值,目标值
x = data.iloc[:, 1:10]
x.head()
y = data["Class"]
y.head()
# 2.3 分割数据
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 3.特征工程(标准化)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.机器学习(逻辑回归)
estimator = LogisticRegression()
estimator.fit(x_train, y_train)
# 5.模型评估
y_predict = estimator.predict(x_test)
y_predict
estimator.score(x_test, y_test)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

很多分类场景当中我们不一定只关注预测的准确率！！！！！

比如以这个癌症举例子！！！我们并不关注预测的准确率，而是关注在所有的样本当中，癌症患者有没有被全部预测（检测）出来。

5 补充：

精确率(Precision)与召回率(Recall)

应用：人脸识别支付：主要提升精确率，更倾向于不能出现错误的预测；预测地震：主要提升召回率，更倾向于宁愿多预测一些错的也不能漏检；

# 四决策树

示例：

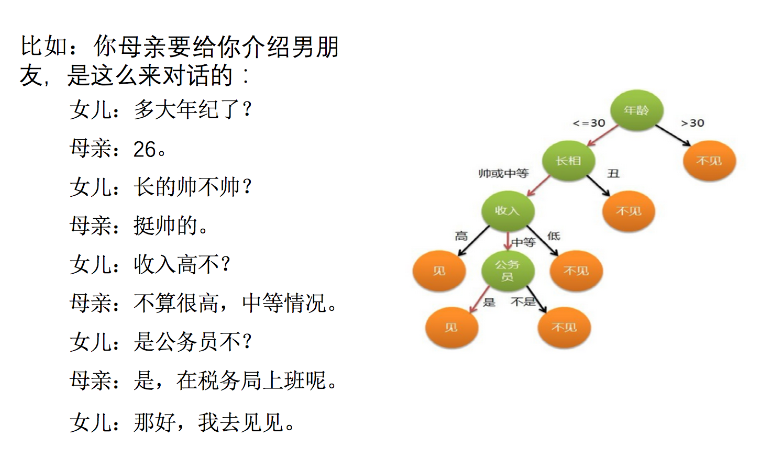
年龄放在主要判断依据；利用这类结构分割数据的一种分类学习方法

原理：信息熵、信息增益

当数据量一致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越高。

"信息熵" (information entropy)是度量样本集合纯度最常用的一种指标。

信息增益：以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏

泰坦尼克号乘客生存预测

代码示例

def decisioncls():
    """
    决策树进行乘客生存预测
    :return:
    """
    # 1、获取数据
    titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")

    # 2、数据的处理
    x = titan[['pclass', 'age', 'sex']]

    y = titan['survived']

    # print(x , y)
    # 缺失值需要处理，将特征当中有类别的这些特征进行字典特征抽取
    x['age'].fillna(x['age'].mean(), inplace=True)

    # 对于x转换成字典数据x.to_dict(orient="records")
    # [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]

    dict = DictVectorizer(sparse=False)

    x = dict.fit_transform(x.to_dict(orient="records"))

    print(dict.get_feature_names())
    print(x)

    # 分割训练集合测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

    # 进行决策树的建立和预测
    dc = DecisionTreeClassifier(max_depth=5)

    dc.fit(x_train, y_train)

    print("预测的准确率为：", dc.score(x_test, y_test))
    return None

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 五集成学习方法之随机森林

集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个数的结果是False, 那么最终投票结果就是True

代码示例

# 随机森林去进行预测
rf = RandomForestClassifier()

param = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}

# 超参数调优
gc = GridSearchCV(rf, param_grid=param, cv=2)

gc.fit(x_train, y_train)

print("随机森林预测的准确率为：", gc.score(x_test, y_test))

1
2
3
4
5
6
7
8
9
10
11

# 六 K-means聚类算法

一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。使用不同的聚类准则，产生的聚类结果不同。

应用:

用户画像，广告推荐，Data Segmentation，搜索引擎的流量推荐，恶意流量识别

基于位置信息的商业推送，新闻聚类，筛选排序

图像分割，降维，识别；离群点检测；信用卡异常消费；发掘相同功能的基因片段

k-means聚类步骤:

1、随机设置K个特征空间内的点作为初始的聚类中心 2、对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别 3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值） 4、如果计算得出的新中心点与原中心点一样（质心不再移动），那么结束，否则重新进行第二步过程

kmean代码示例：

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
1.获取数据
order_product = pd.read_csv("./data/instacart/order_products__prior.csv")
products = pd.read_csv("./data/instacart/products.csv")
orders = pd.read_csv("./data/instacart/orders.csv")
aisles = pd.read_csv("./data/instacart/aisles.csv")
2.数据基本处理

2.1 合并表格
# 2.1 合并表格
table1 = pd.merge(order_product, products, on=["product_id", "product_id"])
table2 = pd.merge(table1, orders, on=["order_id", "order_id"])
table = pd.merge(table2, aisles, on=["aisle_id", "aisle_id"])
2.2 交叉表合并
table = pd.crosstab(table["user_id"], table["aisle"])
2.3 数据截取
table = table[:1000]
3.特征工程 — pca

transfer = PCA(n_components=0.9)
data = transfer.fit_transform(table)
4.机器学习（k-means）
estimator = KMeans(n_clusters=8, random_state=22)
estimator.fit_predict(data)
5.模型评估
silhouette_score(data, y_predict)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 七线性回归

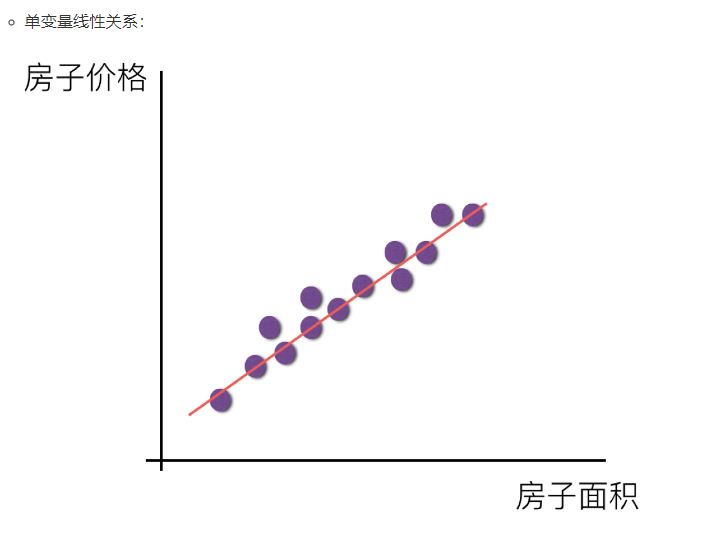
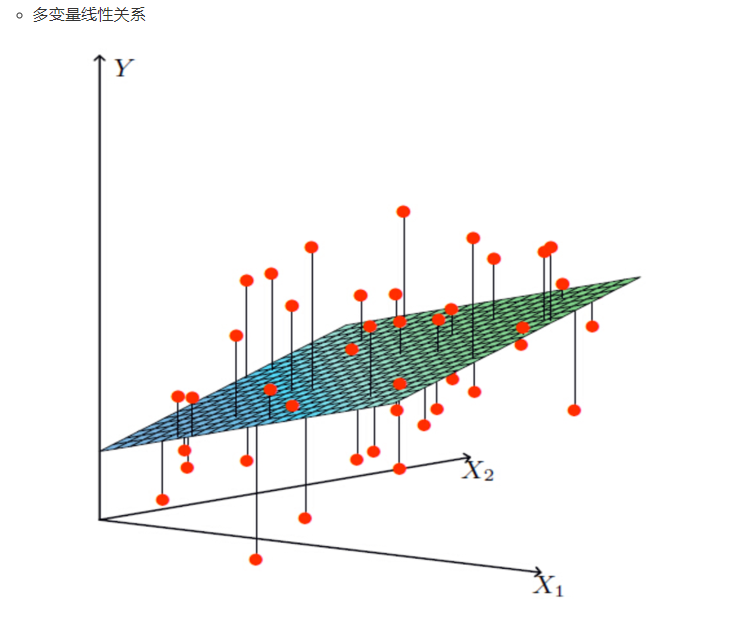
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。

应用场景：房价预测；销售额度预测；贷款额度预测

梯度下降算法：

全梯度下降算法（FG）在进行计算的时候,计算所有样本的误差平均值,作为我的目标函数

随机梯度下降算法（SG）每次只选择一个样本进行考核

小批量梯度下降算法（mini-batch）选择一部分样本进行考核

随机平均梯度下降算法（SAG）会给每个样本都维持一个平均值,后期计算的时候,参考这个平均值

示例：

正规方程：

def linear_model1():
    """
    线性回归:正规方程
    :return:None
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(正规方程)
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

    return None

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

梯度下降法:

def linear_model2():
   """
   线性回归:梯度下降法
   :return:None
   """
   # 1.获取数据
   data = load_boston()

   # 2.数据集划分
   x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

   # 3.特征工程-标准化
   transfer = StandardScaler()
   x_train = transfer.fit_transform(x_train)
   x_test = transfer.fit_transform(x_test)

   # 4.机器学习-线性回归(特征方程)
   estimator = SGDRegressor(max_iter=1000)
   estimator.fit(x_train, y_train)

   # 5.模型评估
   # 5.1 获取系数等值
   y_predict = estimator.predict(x_test)
   print("预测值为:\n", y_predict)
   print("模型中的系数为:\n", estimator.coef_)
   print("模型中的偏置为:\n", estimator.intercept_)

   # 5.2 评价
   # 均方误差
   error = mean_squared_error(y_test, y_predict)
   print("误差为:\n", error)
   return None
   # 我们也可以尝试去修改学习率
    #estimator = SGDRegressor(max_iter=1000,learning_rate="constant",eta0=0.1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

其他了解：正则化线性模型；岭回归等等

← 机器学习算法分类机器学习-资源下载 →

# 机器学习-常见算法

# 一 K-近邻算法(KNN)

# 二 朴素贝叶斯算法

# 三 逻辑回归

# 四 决策树